目录
引
普通的PCA将下式进行特征分解(用论文的话讲就是对角化):
\[ C = \frac{1}{M} \sum \limits_{j=1}^M x_j x_j^T \] 其中\(x_j \in \mathbb{R}^{N}, j = 1, \ldots, M\),且\(\sum \limits_{j=1}^M x_j = 0\)(中心化)。而kernel PCA试图通过一个非线性函数:
\[ \Phi:\mathbb{R}^N \rightarrow F, x \rightarrow X \] 其中\(F\)是一个高维空间(甚至是无限维)。 所以我们要解决这么一个问题:\[ \bar{C} = \frac{1}{M} \sum_{j=1}^M \Phi (x_j) \Phi(x_j)^T \]其实我们面对的第一个问题不是维度的问题而是\(\Phi\)的选择或者说构造。我们为什么要把数据映射到高维的空间?因为当前数据的结构(或者说分布)并不理想。
比如满足\((x-1)^2+(y-1)^2=4\)的点,我们可以扩充到高维空间\((x^2, x, y, y^2)\),在高维空间是线性的(虽然这个例子用在kernel SVM 比较好)。
因为\(\Phi(\cdot)\)的构造蛮麻烦的,即便有一些先验知识。我们来看一种比较简单的泛用的映射:
\[ (x_1, x_2, x_3) \rightarrow (x_1^3, x_2^3, x_3^3, x_1^2x_2,x_1^2x_3,x_1x_2^2,x_1x_3^2,x_2^2x_3,x_2x_3^2,x_1x_2x_3) \] 这种样子的映射,很容易把维度扩充到很大很大,这个时候求解特征问题会变得很麻烦。kernel PCA
假设\(\sum \limits_{i=1}^M \Phi(x_i)=0\)(如何保证这个性质的成立在最后讲,注意即便\(\sum \limits_{i=1}^M x_i = 0\),\(\sum \limits_{i=1}^M \Phi(x_i)=0\)也不一定成立)。
假设我们找到了\(\bar{C}\)的特征向量\(V \ne 0\):
\[ \bar{C}V = \lambda V \] 因为\(V\)是\(\Phi(x_i),i=1,\ldots, M\)的线性组合(这个容易证明),所以,\(V\)可以由下式表示:\[ V = \sum \limits_{i=1}^M \alpha_i \Phi(x_i) \]所以:
\[ \lambda V^T \Phi(x_j) = V^T\bar{C} \Phi(x_j), \quad for \: all \: j=1,\ldots, M \] 等价于(记\(\Phi = [\Phi(x_1), \ldots, \Phi(x_M)]\)):\[ \begin{array}{ll} \lambda \sum \limits_{i=1}^M \alpha_i (\Phi^T(x_i)\Phi(x_j)) &= \lambda \{ \Phi^T \Phi(x_j)\} ^T \alpha \\ & =\frac{1}{M} \sum \limits_{i=1}^M \alpha_i \Phi^T(x_i) \Phi \Phi^T \Phi(x_j) \\ & = \frac{1}{M} \{\Phi^T \Phi \Phi^T \Phi(x_j)\}^T \alpha \end{array} \] 对于\(j=1,\ldots, M\)均成立,其中\(\alpha = [\alpha_1, \ldots, \alpha_M]^T\)。等价于:
\[ M \lambda \Phi^T \Phi \alpha = \Phi^T \Phi \Phi^T \Phi \alpha \] 令\(K = \Phi^T \Phi\),那么可写作:\[ M \lambda K \alpha = K^2\alpha \] 其中\(K_{ij} = \Phi^T(x_i) \Phi(x_j)\)所以,我们可以通过下式来求解\(\alpha\):
\[ M\lambda \alpha = K \alpha \] 即\(\alpha\)是\(K\)的特征向量(注意,当\(\alpha\)为特征向量的时候是一定符合\(M \lambda K \alpha = K^2\alpha\)的,反之也是的,即二者是等价的)。假设\(\lambda_1 \ge \lambda_2 \ge \ldots \ge \lambda_M\)对应\(\alpha^1, \ldots, \alpha^M\),那么相应的\(V\)也算是求出来了。
需要注意的是,\(\|\alpha\|\)往往不为1,因为我们希望\(\|V\|=1\),所以:
\[ V^TV = \alpha^T K \alpha = \lambda \|\alpha\|^2 = 1 \] 所以\(\|\alpha\| = \frac{1}{\sqrt{\lambda}}\)PCA当然需要求主成分,假设有一个新的样本\(x\),我们需要求:
\[ \Phi(x)^TV = \Phi^T(x) \Phi \alpha = \sum \limits_{i=1}^M \alpha_i \Phi^T(x_i) \Phi(x) \]注意,我们只需要计算\(\Phi^T(x_i) \Phi(x)\)。
现在回到kernel PCA 上的关键kernel上。注意到,无论是K,还是最后计算主成分,我们都只需要计算\(\Phi^T(x)\Phi(y)\)就可以了,所以如果我们能够找到一个函数\(k(x,y)\)来替代就不必显示将\(x\)映射到\(\Phi(x)\)了,这就能够避免了\(\Phi(\cdot)\)的选择问题和计算问题。
kernel 的选择
显然,PCA的\(\lambda \ge 0\),所以我们也必须保证\(K\)为半正定矩阵,相应的核函数\(k\)称为正定核,Mercer定理有相应的构建。
也有现成的正定核:
多项式核
\[ k(x, y) = (x^Ty + 1)^d \]
论文中是\((x^Ty)^d\)高斯核函数
\[ k(x, y) = \exp \{\ -\frac{\|x-y\|^2}{2\sigma^2}\} \]
性质
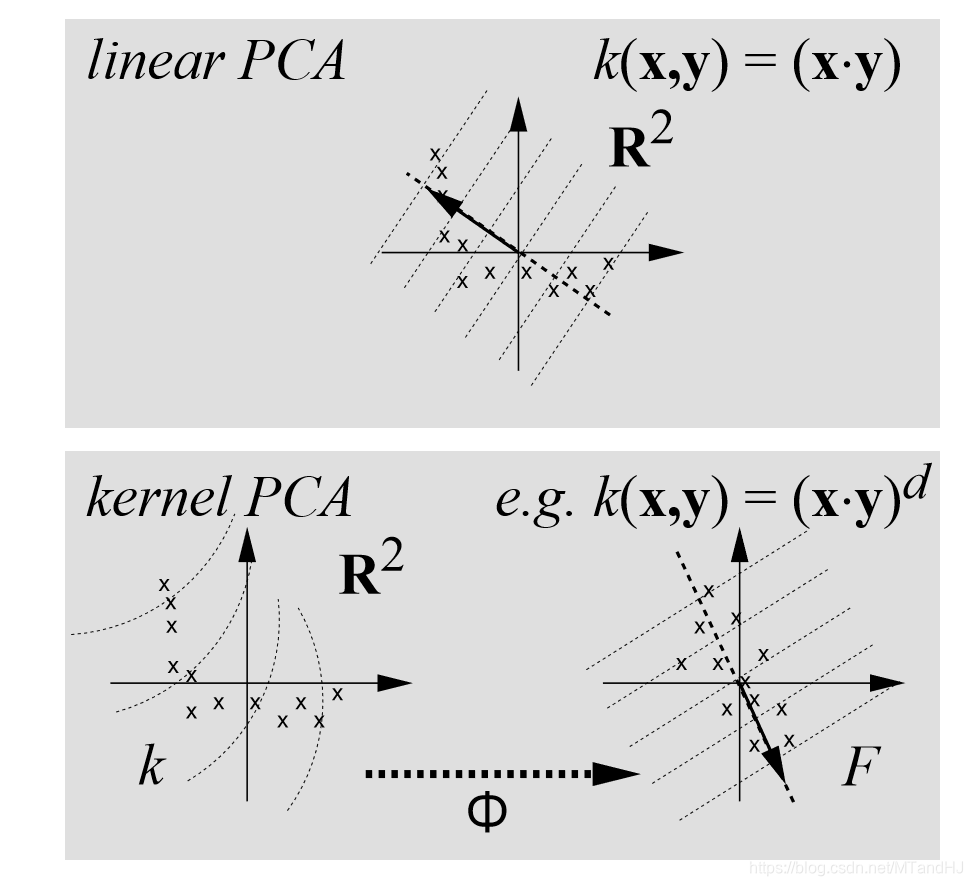
kernel PCA具有普通PCA的性质,良好的逼近(从方差角度),以及拥有最多的互信息等等。并且,如果\(k(x, y) = k(x^Hy)\),那么kernel PCA还具有酉不变性。
因为普通的PCA处理的是一个\(N \times N\)的协方差矩阵,所以,至多获得\(N\)个载荷向量,而kernel PCA至多获得\(M\)个载荷向量(特征值非零)。所以,kernel PCA有望比普通PCA更加精准。
一些问题
中心化
PCA处理的是协方差矩阵,正如我们最开始所假设的,\(\sum \limits_{i=1}^{M} \Phi(x_i)=0\),即中心化。因为\(\Phi(\cdot)\)并不是线性函数,所以,即便\(\sum \limits_{i=1}^M x_i = 0\)也不能保证\(\sum \limits_{i=1}^{M} \Phi(x_i)=0\),不过有别的方法处理。
令\[ \tilde{\Phi}(x_i) = \Phi(x_i) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k) \\ \tilde{K}_{ij} = \tilde{\Phi}^T(x_i) \Phi(x_j) \\ 1_{M} = \{1\}_{ij}^{M \times M} \] 可以得到:\[ \begin{array}{ll} \tilde{K}_{ij} &= \tilde{\Phi}^T(x_i) \Phi(x_j) \\ &= \big(\Phi(x_i) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k)\big)^T \big(\Phi(x_j) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k)\big) \\ &= K_{ij} - \frac{1}{M} \sum \limits_{k=1}^M K_{kj} - \frac{1}{M} \sum \limits_{k=1}^M K_{ik} + \frac{1}{M^2} \sum \limits \limits_{m,n=1}^M K_{mn} \\ &= (K - 1_MK - K1_M + 1_MK1_M)_{ij} \end{array} \] 于是,我们通过\(K\)可以构造出\(\tilde{K}\)。只需再求解\(\tilde{K}\tilde{\alpha} = M \lambda \tilde{\alpha}\)即可。恢复
我们知道,根据PCA选出的载荷向量以及主成分,我们能够恢复出原数据(或者近似,如果我们只选取了部分载荷向量)。对于kernel PCA,比较困难,因为我们并没有显式构造\(\Phi(\cdot)\),也就没法显式找到\(V\),更何况,有时候我们高维空间找到\(V\)在原空间中并不存在原像。
或许, 我们可以通过:\[ \min \limits_{x} \quad \|\Phi(x) - \Phi(\hat{x})\|^2 \] 来求解,注意到,上式也只和核函数\(k(x,y)\)有关。代码
import numpy as npclass KernelPCA: def __init__(self, data, kernel=1, pra=3): self.__n, self.__d = data.shape self.__data = np.array(data, dtype=float) self.kernel = self.kernels(kernel, pra) self.__K = self.center() @property def shape(self): return self.__n, self.__d @property def data(self): return self.data @property def K(self): return self.__K @property def alpha(self): return self.__alpha @property def eigenvalue(self): return self.__value def kernels(self, label, pra): """ 数据是一维的时候可能有Bug :param label: 1:多项式;2:exp :param pra:1: d; 2: sigma :return: 函数 或报错 """ if label is 1: return lambda x, y: (x @ y) ** pra elif label is 2: return lambda x, y: \ np.exp(-(x-y) @ (x-y) / (2 * pra ** 2)) else: raise TypeError("No such kernel...") def center(self): """中心化""" oldK = np.zeros((self.__n, self.__n), dtype=float) one_n = np.ones((self.__n, self.__n), dtype=float) for i in range(self.__n): for j in range(i, self.__n): x = self.__data[i] y = self.__data[j] oldK[i, j] = oldK[j, i] = self.kernel(x, y) return oldK - 2 * one_n @ oldK + one_n @ oldK @ one_n def processing(self): """实际上就是K的特征分解,再对alpha的大小进行一下调整""" value, alpha = np.linalg.eig(self.__K) index = value > 0 value = value[index] alpha = alpha[:, index] * (1 / np.sqrt(value)) self.__alpha = alpha self.__value = value / self.__n def score(self, x): """来了一个新的样本,我们进行得分""" k = np.zeros(self.__n) for i in range(self.__n): y = self.__data[i] k[i] = self.kernel(x, y) return k @ self.__alpha"""import matplotlib.pyplot as pltx = np.linspace(-1, 1, 100)y = x ** 2 + [np.random.randn() * 0.1 for i in range(100)]data = np.array([x, y]).Ttest = KernelPCA(data, pra=1)test.processing()print(test.alpha.shape)print(test.alpha[:, 0])"""